[백준] 1024번 수열의 합 - 시그마 합 공식, 이진탐색 알고리즘(Python)

https://www.acmicpc.net/problem/1024

1024번: 수열의 합

사용 알고리즘

수열의 합공식을 이용해서 리스트를 구하는 조건문을 작성하였다.

풀이

합이 N이면서 길이가 최소 L인 음이 아닌 정수 리스트의 시작 값을 k라고 한다면, 리스트는 항상 [k k+1 k+2 ... k+m](m은 L-1보다 큰 임의의 정수)의 값을 가질 것이다. 따라서 우리는 아래의 식을 만족하는 k, m값을 찾아주면 된다.

<보기 1>

이때, 우리는 등차수열의 유한합 공식이 다음과 같다는 것을 알고있다.

위 공식을 <보기1> 식에 대입시켜 보자.

 

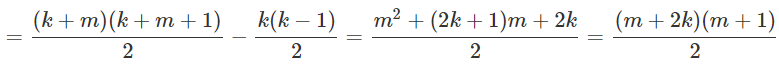
따라서 우리는 N을 만족하는 k, m의 값을 반복문을 통해 찾을 것이다.

 

주의할 점

하지만 입력값 N은1,000,000,000보다 작거나 같은 자연수이므로 단순하게 앞에서부터 맨 뒤까지 탐색을 진행한다면 시간 초과가 될 것이다. 따라서 필자는 이진 탐색 알고리즘을 사용하여 탐색을 진행하였다.(O(longN))

이진 탐색 알고리즘

오름차순으로 정렬된 리스트를 두 부분으로 나누고 필요한 부분에서만 탐색을 진행하는 알고리즘.

예를 들어 0부터 100까지 오름차순으로 정렬된 리스트에서 n이라는 값을 찾고자 할 때, n이 0과 100의 중간값인 50보다 크다면 50~100구간에서, 그렇지 않다면 0~50구간에서 탐색을 진행한다. 한 사이클 마다 리스트의 반을 제외하며 위 과정을 원하는 값을 찾기 때문에 시간복잡도는 O(log N)이다.

 

예외처리

N = 1,000,000,000일 때 이분 탐색을 하게되면 start = 499,999,999 end = 500,000,000인 경우가 생기는데 이때 start+end//2 = 499,999,999가 되어 무한루프에 빠지게 된다. 이는 999,999,999 를 2로 나눈 몫이 499,999,999라서 생기는 현상이다. 이 문제를 없애기 위해 if(k==mid):를 추가하여 이전 mid값과 변화된 mid 값이 똑같다면 무한루프로 간주하고 반복문을 탈출 시켜주었다.

Python

# k = n이 주어졌을 때 임의의 값 k 부터 덧셈을 한다고 가정

# l = k ~ k+m 까지의 길이

import sys

n, l = map(int,input().split())

k=-1

for m in range(l-1,100):

    start = 0

    end = n

    while(end>=0):          #end가 음수가 되면 음수를 포함한 리스트를 출력할 수 있음 ex) 5 5 -> -1 0 1 2 3

        mid = (end + start) // 2

        if(k==mid):         #1,000,000,000을 이분탐색했을때 499999999에서 무한루프 발생

            break

        k = mid

        if((m+2*k)*(m+1)/2 == n):

            for i in range(m+1):

                print(k+i, end=' ')

            sys.exit()

        elif ((m+2*k)*(m+1)/2 < n):

            start = mid+1

        elif ((m+2*k)*(m+1)/2 > n):

            end = mid -1

print(-1)