다중 선형회귀는 단순 선형회귀와 달리 여러개의 독립변수(x)에 의해 결정되는 종속변수(y)를 찾는 모델이다.
y= β0 + β1⋅x0 + β2⋅x1 + β3⋅x2 + β4⋅x3 + ϵ
다중 선형 회귀의 주요 가정은 다음과 같습니다:
- 선형성(Linearity): 독립 변수와 종속 변수 간의 관계가 선형이어야 한다.
- 등분산성(Homoscedasticity): 오차의 분산이 독립 변수의 값에 관계없이 일정해야 한다.
- 독립성(Independence): 오차가 서로 독립적이어야 한다.
- 정규성(Normality): 오차(잔차)가 평균 0이고 정규분포를 따라야 한다.
R의 내장데이터인 mtcar를 사용해 다중선형회귀를 해보자.
> m = mtcars
> res = lm(mpg ~ wt + vs + factor(gear), m)
mpg = β0 + β1⋅wt + β2⋅vs + β3⋅factor(gear)4 + β4⋅factor(gear)5 + ϵ 를 구하는 모델
이때 categorical 데이터인 gear는 3, 4, 5로 구분되며, 기본 기준 수준(reference level)은 gear = 3입니다.
# vs가 이진 변수라면factor()를 사용하지 않아도 올바른 결과를 얻을 수 있으며, 현재 예제에서도 해석은 문제 없음
> res
Call:
lm(formula = mpg ~ wt + vs + factor(gear), data = m)
Coefficients:
(Intercept) wt vs factor(gear)4 factor(gear)5
32.5445 -4.3467 2.4106 1.3538 -0.2035



> summary(res)
Call:
lm(formula = mpg ~ wt + vs + factor(gear), data = m)
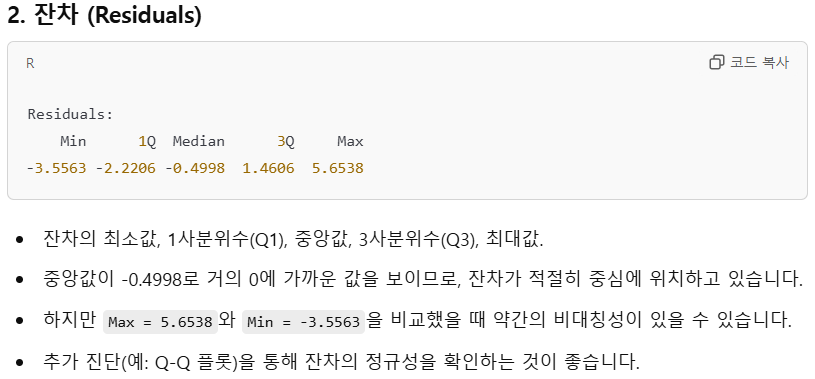
Residuals:
Min 1Q Median 3Q Max
-3.5563 -2.2206 -0.4998 1.4606 5.6538
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 32.5445 3.1915 10.197 9.32e-11 ***
wt -4.3467 0.7639 -5.690 4.81e-06 ***
vs 2.4106 1.4193 1.698 0.101
factor(gear)4 1.3538 1.4809 0.914 0.369
factor(gear)5 -0.2035 1.7464 -0.117 0.908
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
- Intercept:
- 기준 수준(wt = 0, vs = 0, gear = 3)에서 예상 연비는 32.5445.
- 실제 데이터에서 독립 변수들이 0일 가능성은 거의 없으므로, 절편은 비교 기준으로만 의미가 있습니다.
- wt (차량 무게):
- 계수: -4.3467로, 차량 무게가 1 단위 증가하면 연비가 평균적으로 4.3467 감소.
- -값(4.81e-06)이 매우 작아 매우 유의미합니다.
- 차량 무게는 연비에 강한 부정적 영향을 미칩니다.
- vs (엔진 형태):
- 계수: 2.4106. vs = 1(직렬형 엔진)일 때 vs = 0(V형 엔진)보다 연비가 평균적으로 2.4106 높아짐.
- p-값(0.101)이 0.05보다 커서 유의미하지 않음.
- 엔진 형태의 효과가 통계적으로 확신할 만큼 명확하지 않음.
- factor(gear) (기어 수):
- 기어 수 4(gear = 4): 연비가 기준 수준(gear = 3)보다 1.3538 증가. 그러나 p-값(0.369)이 커서 유의미하지 않음.
- 기어 수 5(gear = 5): 연비가 기준 수준(gear = 3)보다 0.2035 감소. 그러나 -값(0.908)이 커서 유의미하지 않음.
Residual standard error: 2.822 on 27 degrees of freedom
Multiple R-squared: 0.8091, Adjusted R-squared: 0.7808
(1) 잔차 표준 오차 (Residual Standard Error):
- 값: 2.822
- 모델이 예측한 값과 실제 값 간의 평균적인 차이를 나타냅니다.
- 이 값이 작을수록 모델이 데이터를 잘 설명합니다.
(2) 결정 계수 (R-squared):
- R2=0.8091R^2 = 0.8091:
- 이 모델은 mpg의 변동성 약 80.91%를 설명합니다.
- 조정된 R2=0.7808R^2 = 0.7808:
- 독립 변수의 개수를 고려한 조정된 결정 계수.
- 여전히 높은 값으로, 모델이 데이터를 잘 설명하고 있음을 보여줍니다.
F-statistic: 28.61 on 4 and 27 DF, p-value: 2.332e-09
(3) F-statistic:
- F-통계량 = 28.61, -값 = 2.332e-09:
- 모델 전체가 통계적으로 유의미하다는 것을 강하게 뒷받침합니다.
- 최소한 하나 이상의 독립 변수가 종속 변수(mpg)에 유의미한 영향을 미칩니다.
함의
주요 변수 : wt(차량 무게)는 연비에 강한 부정적 영향을 미치는 주요 변수로, 매우 유의미한 결과를 보여줍니다.
유의미하지 않은 변수 : vs(엔진 형태) 및 factor(gear)(기어 수)는 통계적으로 유의미하지 않으며, 연비에 큰 영향을 미친다고 보기 어렵습니다.
모델 적합성:R-squared 값이 0.8091로 높으며, 모델이 데이터를 잘 설명.잔차 표준 오차가 적절하며, F-통계량도 모델의 전반적인 유의성을 강하게 뒷받침.
step()의 작동 방식
- 목적: 주어진 초기 모델(res)에서 AIC를 기준으로 독립 변수를 추가하거나 제거하여 가장 간단하고 적합한 모델을 찾습니다.
- AIC(Akaike Information Criterion):
- 모델의 적합도와 복잡도를 평가하는 기준.
- AIC가 낮을수록 더 나은 모델.
- 모델의 복잡도가 증가하면 페널티가 부과되므로, AIC는 적합성과 단순성의 균형을 맞추려 합니다.
> step(res)
Start: AIC=70.95
mpg ~ wt + vs + factor(gear)

Df Sum of Sq RSS AIC
- factor(gear) 2 9.111 224.09 68.283
214.98 70.954
- vs 1 22.968 237.95 72.202
- wt 1 257.783 472.77 94.172
Step: AIC=68.28
mpg ~ wt + vs

Df Sum of Sq RSS AIC
224.09 68.283
- vs 1 54.23 278.32 73.217
- wt 1 405.43 629.52 99.335

Call:
lm(formula = mpg ~ wt + vs, data = m)
Coefficients:
(Intercept) wt vs
33.004 -4.443 3.154

Vif()
> library(car)
> vif(res)
GVIF Df GVIF^(1/(2*Df))
wt 2.175251 1 1.474873
factor(vs) 1.992448 1 1.411541
factor(gear) 2.436001 2 1.249308
10이상이면 심각한 다중공산성문제가 있음 5이상이면 의심단계
# vs의 경우 p val이 0.05보다 작아 영향을 미치지 않는다고 판단하였지만 step의 결과 AIC에 기여를 하므로 빼지 않는 모델이 설명을 더 잘한다고 판단할수 있다.
<모수절약의 법칙>
가능한 작은 수의 독립변수를 이용하여 모형을 구축해야한다는 원칙
모델간 적합성 비교
> install.packages("lmtest")
> library(lmtest)
> model1 = lm(finalgrade ~ per2grade,g)
> model2 = lm(finalgrade~per1grade+per2grade,g)
> lrtest(model1, model2)
이때 model1과 model2는 반드시 중첩되어야 한다. 즉, 단순한 모델은 복잡한 모델의 특별한 경우여야 한다.
> lrtest(model1, model2)
Likelihood ratio test
Model 1: finalgrade ~ per1grade
Model 2: finalgrade ~ per1grade + per2grade
#Df LogLik Df Chisq Pr(>Chisq)
1 3 -1308.8
2 4 -1070.7 1 476.18 < 2.2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
- 귀무가설 (H0H_0): "단순 모델(Model 1)로 충분하다. 복잡한 모델(Model 2)은 추가적인 설명력을 제공하지 않는다."
- 대립가설 (H1H_1): "복잡한 모델(Model 2)이 단순 모델(Model 1)보다 데이터를 더 잘 설명한다."
해석:
- pp-값이 <0.001< 0.001로 매우 작으므로 귀무가설을 기각.
- 복잡한 모델(Model 2)이 단순한 모델(Model 1)보다 데이터를 유의미하게 더 잘 설명한다는 결론.
- LogLik:
- 로그 우도 값(Log-Likelihood). 값이 클수록 모델이 데이터를 더 잘 설명.
- Model 1: -1308.8
- Model 2: -1070.7 → Model 2가 더 좋은 적합도를 가짐.
복잡한 모델(Model 2)이 단순 모델(Model 1)보다 통계적으로 유의미하게 더 적합하다고 판단됩니다.
'R 통계' 카테고리의 다른 글
| [R] 상관분석 (0) | 2024.12.05 |
|---|---|
| [R] 로지스틱회귀 (0) | 2024.11.24 |
| [R] 단순선형회귀 (0) | 2024.11.23 |
| [R] 독립된 세 집단 이상의 모평균 비교 (1) | 2024.10.19 |
| [R] 독립된 두 집단의 모평균 비교 (0) | 2024.10.19 |



