R의 survival 패키지에 포함된 colon 데이터셋은 결장암 환자에 대한 임상 데이터를 제공하며, 생존 분석(survival analysis)에 주로 사용됩니다. 이 데이터셋은 결장암 연구에서 환자의 상태와 치료 결과를 기록한 데이터입니다.
> library(survival)
> library(descr)
> df = colon
odds = P / 1 - P = (사건이 일어날 확률) / (사건이 일어나지 않을 확률)
위 데이터의 경우

로지스틱회귀와의 연관성

> m = glm(status ~ obstruct, family = binomial, data = df)
> summary(m)
Call:
glm(formula = status ~ obstruct, family = binomial, data = df)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -0.06945 0.05171 -1.343 0.179
obstruct 0.25891 0.11783 2.197 0.028 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1


(Dispersion parameter for binomial family taken to be 1)
Null deviance: 2575.6 on 1857 degrees of freedom
Residual deviance: 2570.7 on 1856 degrees of freedom
AIC: 2574.7
Number of Fisher Scoring iterations: 3

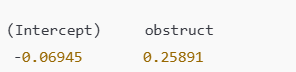
> round(exp(cbind(coef(m), confint(m))),3)
Waiting for profiling to be done...
2.5 % 97.5 %
(Intercept) 0.933 0.843 1.032
obstruct 1.296 1.029 1.633
1. coef(): 회귀 계수 추출
- coef(m)는 로지스틱 회귀 모델 mm에서 회귀 계수를 추출하는 함수입니다.
- 로지스틱 회귀 모델의 계수는 log(Odds Ratio)\log(\text{Odds Ratio}) 형태로 제공됩니다.
- 각 계수는 독립 변수가 종속 변수에 미치는 영향을 나타냅니다:
- 양수 계수: 독립 변수가 증가할수록 사건 발생 확률(오즈)이 증가.
- 음수 계수: 독립 변수가 증가할수록 사건 발생 확률(오즈)이 감소
2. confint(): 신뢰구간 계산
- confint(m)는 모델 mm에서 계수의 신뢰구간을 계산합니다.
- 기본적으로 95% 신뢰구간을 제공합니다.
- 신뢰구간은 계수의 추정값이 실제 값(모수)을 포함할 가능성이 있는 범위를 나타냅니다.
- 상한과 하한이 1을 포함하지 않으면 해당 계수는 통계적으로 유의미.

3. exp(): 지수화로 Odds Ratio 계산
로지스틱 회귀의 계수는 log(Odds Ratio)\log(\text{Odds Ratio})로 제공되므로, 지수화(exp\exp)하여 Odds Ratio로 변환합니다.

다중 로지스틱 회귀
이번에는 x값이 여러개인 로지스틱회귀 분석을 해보자
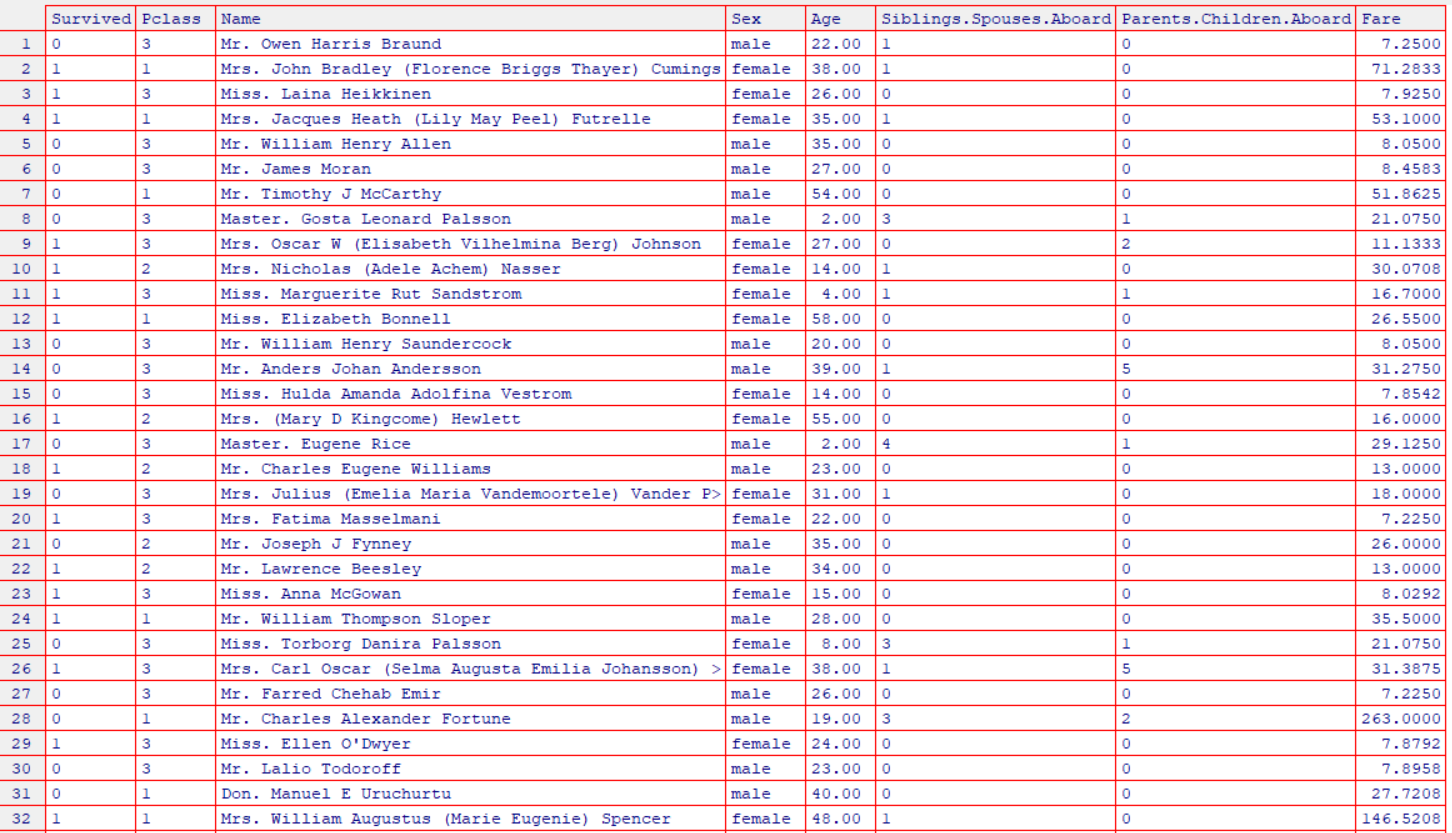
위의 데이터는 타이타닉 데이터 셋으로 생존, 좌석의 등급, 이름, 성별, 나이, 동승한 형제자매의 수, 동승한 부모자식의 수, 지불한 요금으로 구성되어 있다.
이름빼고 결측치빼고 성별 클래스 factor로 바꿔주고 등등 전처리하고 glm을 돌려보면
> model = glm(survived~sex+pclass+age+sibsp+parch+fare,data=data1,family = binomial)
> summary(model)
Call:
glm(formula = survived ~ sex + pclass + age + sibsp + parch +
fare, family = binomial, data = data1)
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) 1.353067 0.410855 3.293 0.000990 ***
sex1 2.756710 0.200642 13.739 < 2e-16 ***
pclass2 -1.161491 0.300960 -3.859 0.000114 ***
pclass3 -2.350022 0.304666 -7.713 1.22e-14 ***
age -0.043410 0.007790 -5.573 2.51e-08 ***
sibsp -0.401572 0.110795 -3.624 0.000290 ***
parch -0.106884 0.118767 -0.900 0.368151
fare 0.002823 0.002468 1.144 0.252771
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1182.77 on 886 degrees of freedom
Residual deviance: 780.93 on 879 degrees of freedom
AIC: 796.93
Number of Fisher Scoring iterations: 5
-step()사용 후
> step(model)
Start: AIC=796.93
survived ~ sex + pclass + age + sibsp + parch + fare
Df Deviance AIC
- parch 1 781.75 795.75
- fare 1 782.37 796.37
<none> 780.93 796.93
- sibsp 1 796.79 810.79
- age 1 815.20 829.20
- pclass 2 847.84 859.84
- sex 1 1020.26 1034.26
Step: AIC=795.75
survived ~ sex + pclass + age + sibsp + fare
Df Deviance AIC
- fare 1 782.82 794.82
<none> 781.75 795.75
- sibsp 1 801.56 813.56
- age 1 815.88 827.88
- pclass 2 852.19 862.19
- sex 1 1024.08 1036.08
Step: AIC=794.82
survived ~ sex + pclass + age + sibsp
Df Deviance AIC
<none> 782.82 794.82
- sibsp 1 801.59 811.59
- age 1 818.25 828.25
- pclass 2 900.80 908.80
- sex 1 1031.69 1041.69
Call: glm(formula = survived ~ sex + pclass + age + sibsp, family = binomial,
data = data1)
Coefficients:
(Intercept) sex1 pclass2 pclass3 age sibsp
1.55615 2.73802 -1.32170 -2.54124 -0.04392 -0.40962
Degrees of Freedom: 886 Total (i.e. Null); 881 Residual
Null Deviance: 1183
Residual Deviance: 782.8 AIC: 794.8
최종 모델은 다음과 같습니다:

- 성별(sex):
- 회귀계수 β=2.73802\beta = 2.73802: 여성일 때 생존할 확률이 남성보다 유의미하게 높습니다.
- e2.738≈15.45e^{2.738} \approx 15.45: 여성의 생존 오즈는 남성의 약 15.45배입니다.
- 승객 등급(pclass):
- pclass2: 2등급은 1등급에 비해 생존 확률이 낮습니다.
- pclass3: 3등급은 1등급에 비해 생존 확률이 더욱 낮습니다.
- 회귀계수가 클수록 생존에 불리한 영향을 미칩니다.
- 나이(age):
- 나이가 많을수록 생존 확률이 감소합니다.
- β=−0.04392\beta = -0.04392: 나이가 1살 증가할 때 로그 오즈가 감소하지만, 영향력은 비교적 작습니다.
- 형제자매/배우자 수(sibsp):
- 동반한 사람이 많을수록 생존 확률이 감소합니다.
- 이는 혼란스러운 상황에서 가족 구성원이 많으면 구조에 불리할 수 있음을 시사합니다.
> round(exp(coef(model2)),3)
(Intercept) sex1 pclass2 pclass3 age sibsp
4.741 15.456 0.267 0.079 0.957 0.664
각각 변수들의 오즈비
등분산성 평가
> vif(model2)
GVIF Df GVIF^(1/(2*Df))
sex 1.151231 1 1.072955
pclass 1.467610 2 1.100659
age 1.478935 1 1.216115
sibsp 1.168421 1 1.080935
'R 통계' 카테고리의 다른 글
| [R] 카이제곱검정 (0) | 2024.12.05 |
|---|---|
| [R] 상관분석 (0) | 2024.12.05 |
| [R] 다중 선형회귀 (0) | 2024.11.24 |
| [R] 단순선형회귀 (0) | 2024.11.23 |
| [R] 독립된 세 집단 이상의 모평균 비교 (1) | 2024.10.19 |


